※このページでは、数式を表示するためにJavaScriptを使用しています。
特定の相手にメッセージを秘匿して送信する場合,メッセージの内容を第三者には解読できない形に 変換して送信します.このように,元のメッセージを変換する処理を暗号化と言い,変換されたメッセージ を暗号,または暗号文と言います.暗号化されていない元のメッセージは平文と言います.一方,メッセージ を受け取る受信者側は,暗号文のままではメッセージの内容がわからないので,暗号文を元のメッセージ に戻す必要があります.このように,暗号文から元のメッセージに逆変換する処理を復号,または復号化 と言います.
暗号の歴史は古く,古代ローマ時代から暗号が使われてきました.有名な暗号方式にシーザー暗号と 呼ばれるものがあります.この暗号方式はアルファベットの文字を3つ後方へシフトするものです.例えば, 文字AならばDに,BならばEに,CならばFに,という具合にアルファベット順で3つ後の文字に置換するもの です.受け取った暗号を復号するには,受け取ったアルファベットを前方に3つシフトすればよいわけです. このシーザー暗号において,アルファベットを一定数シフトするということがアルゴリズムで,シフトする 量の3という数値がこの暗号の鍵になります.アルゴリズムと鍵はメッセージをやり取りする当事者以外には 知られないように秘匿しなければなりません.
暗号において,アルゴリズムと鍵が重要なファクターなります.
暗号方式には,共通鍵暗号方式と公開鍵暗号方式があります.共通鍵暗号方式は,暗号化の鍵と復号化 の鍵は同じものを使います.

図1. 共通鍵暗号方式
先に紹介したシーザー暗号は共通鍵暗号方式に分類されます.シフト量3が暗号化と復号化の処理で共通 した鍵となっているからです.シーザー暗号はアルゴリズムが単純で,現在では使われることがありません. 共通鍵暗号方式で代表的なものにAESというものがありますが,ここではその内容の説明は省略します.
これに対して,公開鍵暗号方式というものがあります.
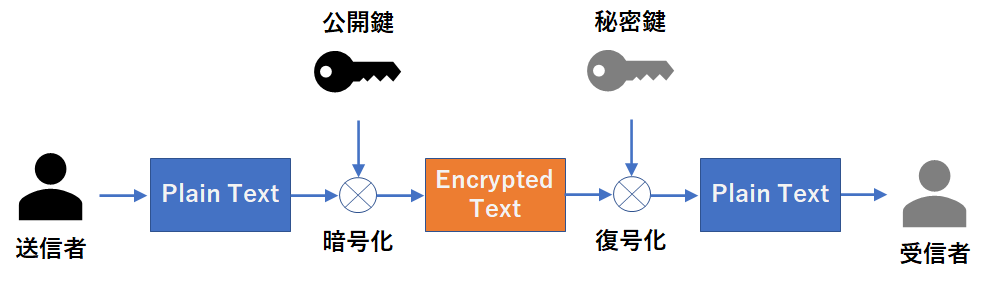
図2. 公開鍵暗号方式
暗号を使って伝送路でメッセージを送受信する場合,暗号化の鍵の送信が問題になります.なぜならば, 鍵そのものを暗号化して送信するわけにはいかないからです.公開鍵暗号方式では,暗号化の鍵を公開する ことが前提となっているので,鍵の受け渡し時に盗聴されても問題にはなりません.復号化の鍵はメッセージ の受信者のみが保持していればよいので,伝送路に送信されることはありません.このような仕組みから 公開鍵暗号方式は共通鍵暗号方式よりも安全性が高いものと言えます.
RSA暗号は,公開鍵暗号方式の代表的なもので,1977年にRivest, Shamir, Adlemanの3人によって開発され ました.この3人の名前の頭文字を取ってRSA暗号と名づけられました.RSA暗号は秘密鍵として2つの巨大な 素数を使用し,公開鍵としてそれら2つの素数の合成積を使用します.RSA暗号の安全性は,この巨大な合成積 を素因数分解することが極めて困難であることに帰着しています.これにより,2つの素数の合成積を公開して もそこから素因数分解によって,2つの素数そのものを得ることが現実的には不可能となっています.
なぜ素因数分解が困難であるかというと,素因数分解を効率的に実行するアルゴリズムが今のところ存在 しないからです.例えば,素数11と17の積187を素因数分解する場合,2,3,5,$\cdots$と小さい素数から順番 に除算を実行して187を割り切る素数を探っていきます.この程度の小さな数であれば,紙と鉛筆を使った筆算 でもすぐに素因数分解することができます.しかし,RSA暗号では1024 bitや2048 bitといった巨大な素数を 使用しています.これらの素数の積は3072 bitの合成数になります.このような巨大な合成数を同じやり方で 素因数分解を施行すると,スーパーコンピューターを使ってもとてつもない時間がかかります.
実際に計算時間を見積もってみます.上記の3072 bitの合成数を素因数分解する場合,小さいほうの1024 bitの素数を見つけることができれば,もう一方の素数も見つけることができます.素数のみを選択して除算を 実行するのは実際には不可能ですが,仮にこれが可能だったとします.任意の正の整数$n \in \mathbb{N}$以下 の素数の個数は素数定理を使って見積もることができます.証明は省きますが,素数定理は以下のようになり ます.
素数定理
任意の自然数$n \in \mathbb{N}$以下の素数の個数$\pi(n)$は以下のように近似することができる.
\[ \pi(n) \fallingdotseq \int^n_2{\frac{dx}{\ln x}} \fallingdotseq \frac{n}{\ln n} + \mathcal{O} \left( \frac{1}{(\ln n)^2} \right) \]ここで,$\mathcal{O}(\cdot)$はランダウ記号を表す.
ここで$n = 2^{1024}$となるので,素数の個数は
\[ \pi(2^{1024}) \fallingdotseq \frac{2^{1024}}{\ln 2^{1024}} \fallingdotseq 2.5327 \times 10^{305} \]となります.すなわち,除算を$2.5327 \times 10^{305}$回実行して1024 bitの素数を見つけることができ ます.仮に除算1回当たり1 nsecで実行できるものとします.すると,実行時間は$2.5327 \times 10^{305} \times 10^{-9} = 2.5327 \times 10^{296}$ secとなります.1年間は$365 \times 24 \times 3600 = 31536000$ secとなるので,1024 bitの素数を得るのに$2.5327 / 3.1536 \times 10^{289} \fallingdotseq 8.0311 \times 10^{288}$年も処理時間がかかります.先にも述べましたように,素数だけを 選んで除算することは不可能ですので,この見積もりはかなり処理時間を短く見積もったものになります. したがって,公開鍵である合成数を素因数分解して2つの素数を得ることは,事実上不可能であることがわか ります.
RSA暗号において,2つの素数とその合成積がそれぞれ秘密鍵と公開鍵としてどのように機能しているか, その概要を見ていきます.RSA暗号の暗号化と復号化にはべき剰余演算を使います.べき剰余演算とは,任意の 数のべき乗を2つの素数の合成積によって,その剰余を計算します.
初めに,下表をご覧ください.この表は1から9までのそれぞれの数値のべき剰余演算を1乗から37乗(途中 省略)まで計算した結果を記したものです.
2つの素数としては13と19を使用しています.この2つの素数の積は247なので,1から9までの数値の べき乗した値を247で割った余りを記しています.
| べき乗 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 3 | 1 | 8 | 27 | 64 | 125 | 216 | 96 | 18 | 235 |
| 4 | 1 | 16 | 81 | 9 | 131 | 61 | 178 | 144 | 139 |
| 5 | 1 | 32 | 243 | 36 | 161 | 119 | 11 | 164 | 16 |
| 6 | 1 | 64 | 235 | 144 | 64 | 220 | 77 | 77 | 144 |
| 7 | 1 | 128 | 211 | 82 | 73 | 85 | 45 | 122 | 61 |
| 8 | 1 | 9 | 139 | 81 | 118 | 16 | 68 | 235 | 55 |
| 9 | 1 | 18 | 170 | 77 | 96 | 96 | 229 | 151 | 1 |
| 35 | 1 | 124 | 165 | 62 | 99 | 206 | 106 | 31 | 55 |
| 36 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 37 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
上記の表のべき乗の値が37のところをご覧ください.すべての数値が元の数値に戻っていることがわか ります.すなわち,1乗から始まって,36乗を周期としてべき剰余の値が元の数値と等しくなります.任意の 正の整数を$v$とすると,$36v + 1$乗ごとに元の数値が出現します.
例えば,9という数値を暗号化する場合,9の5乗の剰余である16に変換します.これを復号する場合, 16の適当の数のべき乗値を求めて剰余を計算するわけですが,このべき乗をdとすると, \[ 5d = 36v + 1 \] という方程式が成り立ちます.この方程式の1つの解がd = 29となるので,16を29乗した値を求めます. \[ 16^{29} = 83,076,749,736,557,242,056,487,941,267,521,536 \] 上記の値を2つの素数13と19の積247の剰余を求めると,確かに9になります.
この例はあくまでRSA暗号の原理を説明するために,小さな素数を使っていますが,実際は10進数で300桁 以上の素数を使っているので,べき剰余演算で元の数値に戻る周期も同じぐらい巨大な値となります.次の章 からRSA暗号がなぜ暗号として成り立っているのか,数学的に厳密に説明します.
前の章では,べき剰余演算でべき乗の数を増やしていくと,ある周期で元の数値に戻るという性質を見ま した.このような現象はどうして起きるのでしょうか?実はこのことは整数論の定理によって論理的に説明する ことができます.初めに,以下に示すFermatの定理をご覧ください.
Fermatの定理
任意の素数$p$と$p$の倍数ではない自然数$a \in \mathbb{N}$について,以下の合同式が成り立つ. \[ a^{p - 1} \equiv 1(\mathrm{mod} \ p) \]
Fermatの定理はその証明が大学入試の問題になるぐらい有名な定理ですので,ご存知の方も多いと思い ます.ここでは,その証明は割愛します.Fermatの定理の合同式を変形すると,
\[ a^p \equiv a (\mathrm{mod} \ p) \]
が得られます.すなわち,素数$p$の倍数ではない任意の自然数$a$の$p$乗を$p$で割った余りは,$a$を $p$で割った余りと等しいということがわかります.$a < p$となるように$p$を選べば,$a^p$を$p$で割った 余りは元の自然数$a$になります.そして,元の自然数$a$と等しくなるべき剰余演算のべき乗周期は$p - 1$とな ります.
合同式において,素数$p$のことを法と呼びます.べき剰余演算が素数を法とすると,元の数値に戻ると いう性質は,法が素数の場合に限られるのでしょうか?合成数ではこのようなことは起きないのでしょうか? 実はこのような性質は法が合成数の場合でも成り立つことが,Eulerによって証明されました.それが以下の 示すEulerの定理です.
Eulerの定理
任意の自然数$a \in \mathbb{N}$と互いに素となる自然数$n$について,以下の合同式が成り立つ. \[ a^{\varphi(n)} \equiv 1(\mathrm{mod} \ n) \]
ここで,$\varphi(n)$はEuler関数というもので,自然数$n$以下の$n$と互いに素となる自然数の個数を 示す関数である.
Euler関数について説明を捕捉します.$n$が素数である場合,$n - 1$以下の自然数と$n$は互いに素と なるので,$\varphi(n) = n - 1$となります.そして,この場合はFermatの定理と一致した結果が得られます. 次に$n$が2つの異なる素数$p$と$q$の合成数だった場合を考えます.$n$と互いに素ではない$n$以下の数は $n$以下の$p$の倍数と$q$の倍数であるので,これを羅列すると, \begin{align*} p, \ 2p, \ \cdots, \ p(q - 1), \ pq \\ q, \ 2q, \ \cdots, \ (p - 1)q, \ pq \end{align*} となります.上下段で共通している数は$pq$のみであるので, \[ \varphi(n) = pq - p - q + 1 = (p - 1)(q - 1) \] となります.
一般的に$n = p_1^{e_1} \cdots p_r^{e_r}$と素数$p_1, \cdots, p_r$によって素因数分解された場合, \[ \varphi(n) = (p_1^{e_1} - p_1^{e_1 - 1}) \cdots (p_r^{e_r} - p_r^{e_r - 1}) = \prod_{k = 1}^{r}{(p_k^{e_k} - p_k^{e_k - 1})} = \prod_{k = 1}^{r}{p_k^{e_k - 1}(p_k - 1)} \] となります.
以下にEulerの定理の証明を記します.
【証明】
自然数$n$と互いに素な$n$以下の自然数の集合を$A = \left\{ m_1, m_2, \cdots, m_{\varphi(n)} \right\}$とする.$i \ne j$のとき,$m_i \not \equiv m_j (\mathrm{mod} \ n)$である.なぜならば, $m_i \equiv m_j (\mathrm{mod} \ n)$ならば,$m_i - m_j$は$n$の倍数となり,$m_i, m_j < n$である ことから,$m_i = m_j$となってしまうからである.集合$A$の各要素に$n$と互いに素となる自然数$a$を 掛けたものを要素とする集合を$B$とすると, \begin{align*} B = \left\{ am_1, am_2, \cdots, am_{\varphi(n)} \right\} \end{align*} となる.集合$B$の各要素についても,$i \ne j$のとき,$am_i \not \equiv am_j (\mathrm{mod} \ n)$ である.したがって,集合$A$と集合$B$は$n$を法として合同である. 集合$A$と集合$B$の各要素をすべて掛け合わせたものも$n$を法として合同となるので, \begin{align*} am_1 \cdot am_2 \cdots am_{\varphi(n)} & \equiv m_1 \cdot m_2 \cdots m_{\varphi(n)} (\mathrm{mod} \ n) \\ a^{\varphi(n)}m_1 \cdot m_2 \cdots m_{\varphi(n)} & \equiv m_1 \cdot m_2 \cdots m_{\varphi(n)} (\mathrm{mod} \ n) \\ \therefore a^{\varphi(n)} & \equiv 1 (\mathrm{mod} \ n) \end{align*} が成り立つ.
RSA暗号の暗号化と復号化の原理は前節で示したEulerの定理に基づいています.ここで,2つの異なる素数を$p, q$とし,その合成積を$n = pq$とします.また,暗号化されていない平文を$M$,暗号文を$C$とします.適当なべきの値$e, d$によって, \begin{align*} M^e \equiv C (\mathrm{mod} \ n) \\ C^d \equiv M (\mathrm{mod} \ n) \end{align*} とすることができます.これら2つの合同式をまとめると, \[ M^{ed} \equiv M (\mathrm{mod} \ n) \] となります.また,Eulerの定理より,$M$と$n$が互いに素であれば, \[ M^{\varphi(n)} \equiv 1 (\mathrm{mod} \ n) \] が成り立ちます.$M < n$となるようにすれば, \[ M^{\varphi(n) v + 1} \equiv M (\mathrm{mod} \ n) \] が成り立ちます.ただし,ここで$v$は整数です.
受信者側,すなわち復号する側にとって未知数は何かというと,$d$と$v$になります.$d$の値がわかれば 暗号文$C$から平文$M$を得ることができます.$d$の値を求めるには,以下の不定方程式を解く必要があります. \[ ed = \varphi(n)v + 1 \]
さて,ここで上記の方程式がいつでも整数解$(d, v)$を持つかが問題になります.このことについては, 以下の不定方程式の整数解の存在定理によって保障されています.
不定方程式の整数解の存在定理
整数$a, b$を係数とする以下の方程式が整数解を持つための必要十分条件は, $a$と$b$が互いに素であることである. \[ ax + by = 1 \]
【証明】
必要性
$a$と$b$が互いに素でないとき,$a$と$b$の最大公約数$d \geq 2$が存在する.方程式の左辺は$d$の 倍数となるが,右辺は$d$の倍数とはならず矛盾する.したがって,$a$と$b$は互いに素である.
十分性
$a$と$b$が互いに素であるとすると,$a, 2a, \cdots, (b - 1)a$を$b$で割ると,余りはすべて異なる. したがって,この中に余りが$1$となるものが存在する.これを$ma$とおき,$b$で割ったときの商を$n$ とすると, \[ ma = nb + 1 \] となる.これを変形すると, \[ am - bn = 1 \] となり,与えられた方程式の整数解$(m, -n)$が存在する.
$a = e, b = \varphi(n)$とすると,$e$と$\varphi(n)$が互いに素であれば,$ed = \varphi(n)v + 1$を 満たす整数$d$が存在します.$\varphi(n) = (p - 1)(q - 1)$であるから,$e$と$\varphi(n)$が互いに素であ るためには,$e$が$p - 1$と$q - 1$に対してそれぞれ互いに素でなくてはなりません.
さて,前章で1から9までの数値のべき剰余を求めて,どこで元の値と一致するかを見ました.実際にEuler の定理に従っているかを見てみます.
使用している2つの素数は$p = 13, q = 19$なので,$n = 13 \cdot 19 = 247$となります.平文を $M = 9$とし,暗号化のためのべきの値を$e = 5$とすると,暗号文は$C = 16$となります.Euler関数の値は $\varphi(247) = 12 \cdot 18 = 216$となります.前章の表では,べき乗される底の値が元に戻る周期は36 でした.Euler関数の値よりも小さな値となっています.実はEulerの定理は十分条件のみを示しています. したがって,べき乗して元の値に一致する周期の最小値は必ずしも$\varphi(n)$ではありません.
Eulerの定理をさらに精緻化したCamichaelの定理というものがあります.以下にこれを紹介します.
Carmichaelの定理
任意の自然数$a \in \mathbb{N}$と互いに素となる自然数$n$について,以下の合同式が成り立つ. \[ a^{\lambda(n)} \equiv 1(\mathrm{mod} \ n) \]
ここで,$\lambda(n)$はCarmichael関数というもので,以下の性質を持つ関数である.
$n = 2^e$のとき,
\[
\lambda(2^e) =
\begin{cases}
1 \ \ & e = 1 \\
2 \ \ & e = 2 \\
2^{e - 2} \ \ & e \geq 3
\end{cases}
\]
$n$が奇素数$p (\geq 3)$のべき乗,すなわち$n = p^e$のとき,
\[
\lambda(p^e) = p^{e - 1} (p - 1)
\]
また,$n$が素数$p_1, \cdots, p_m$によって,$n = {p_1}^{e_1} \cdots {p_m}^{e_m}$と素因数分解される
とき,
\[
\lambda({p_1}^{e_1} \cdots {p_m}^{e_m}) = \mathrm{lcm}(\lambda({p_1}^{e_1}), \cdots,
\lambda({p_m}^{e_m}))
\]
ただし,$\mathrm{lcm}(\lambda({p_1}^{e_1}), \cdots, \lambda({p_m}^{e_m}))$は$\lambda({p_1}^{e_1}),
\cdots, \lambda({p_m}^{e_m})$の最小公倍数を表す.
先の例における$n = 13 \cdot 19$をCarmichael関数に代入してみます. \begin{align*} \lambda(13 \cdot 19) & = \mathrm{lcm}(\lambda(13), \lambda(19)) \\ & = \mathrm{lcm}(12, 18) \\ & = 36 \end{align*} このように,先の例におけるべきの周期とCarmichael関数の値が一致しました.
一般的に2つの素数$p, q$は数百桁の巨大な素数なので,$p - 1$と$q - 1$を素因数分解すること は困難です.したがって,$p - 1$と$q - 1$の最小公倍数を計算することも困難です.RSA暗号で復号化の鍵を 計算するにはEuler関数を使えば十分と考えられます.
