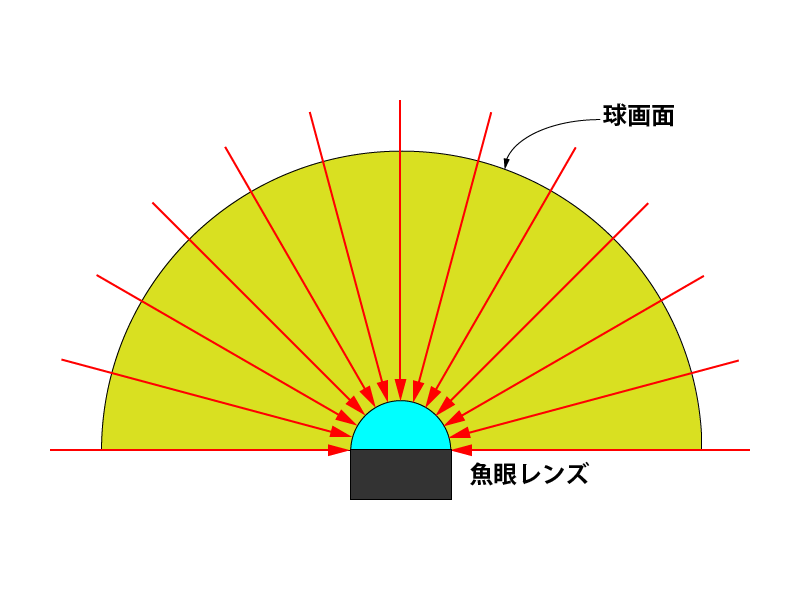
全方位カメラは魚眼レンズを使ったカメラで、レンズを中心とした半球面のすべての方向からの 光を取り込んで、CMOSやCCDなどの撮像素子の上で平面画像を結像します。

撮像した画像は下記のような円周画像となります。

　画像を見てお分かりのように魚眼レンズで取り込んだ画像は、円の中心部分では歪みは小さいですが、 円の周辺部分では歪みが大きくなっています。また、本来は直線に並んでいる蛍光灯が、円形に歪んでいます。 このように全方位カメラは魚眼レンズによって、3次元の半球面の画像を2次元の円画像にマッピングして います。そのため、画像は大きく円形に歪むのが特徴です。

　このように円画像のままですと、歪があるので人間にとっては見にくい画像となっています。したがって、 全方位カメラには画像を補正する機能を備えたものもあります。この場合、歪んだ円画像を一気に補正するのは 困難なので、特定の領域を切り出して補正します。

　図3に示された円画像の①と②の領域を補正すると、図4と図5のように歪の取れた画像が 得られます。特に蛍光灯の部分を見てもらえればわかりますが、オリジナルの円画像では楕円形に蛍光灯の 並びが歪んでいますが、補正後の画像では、蛍光灯が直線に並んでいます。

　ここでは、魚眼レンズによってできた画像を補正する方法についてご紹介します。

　魚眼レンズによる円画像を補正するためには、円画像を仮想的な球面スクリーン上に逆投影し、その球面スクリーンに接する平面に対して球面スクリーンの画像を投影するという方法を取ります。この接平面が補正された画像を映し出すディスプレイに相当します。このように、画像補正は地球儀から平面の地図帳を作るのと同じ方法を取るわけです。

　この節では、実際に円画像からどのようにして補正画像を作り出すかについて、具体的な方法を記します。

　円画像から補正した画像を作るためには、接平面上の点$(u, v)$に対応する円画像上の点$(x, y)$を計算しなければなりません。そのためには以下の手順で計算されます。

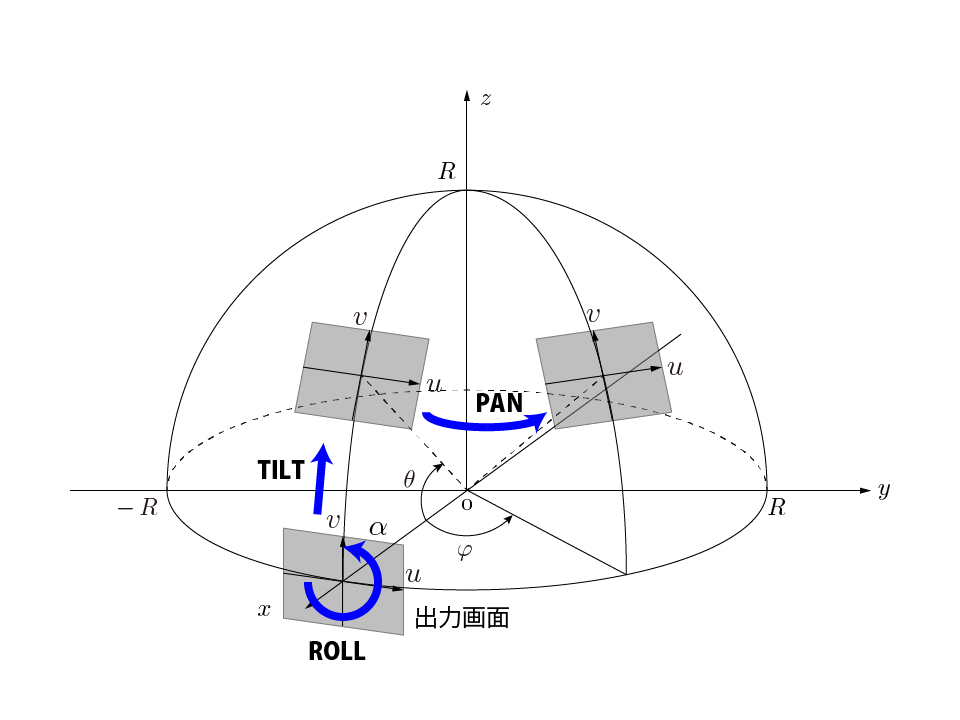
　下の図は接平面を基準となる位置から、どのように移動させれば目標の位置に到達できるかを表したものです。基本的には$x$軸、$y$軸、および$z$軸の周りの回転移動を組み合わせることになります。

　以下の手順で接平面を回転させると、球面スクリーン上の任意の点に接平面を移動することができます。

　上記の手順をズームと回転の行列を使って表現すると、以下のようになります。

\begin{align} \left( \begin{array}{c} x' \\ y' \\ z' \end{array} \right) = \underbrace{ \left( \begin{array}{ccc} \cos \varphi & -\sin \varphi& 0 \\ \sin \varphi & \cos \varphi & 0 \\ 0 & 0 & 1 \end{array} \right) }_{\mathrm{PAN}} \underbrace{ \left( \begin{array}{ccc} \cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta \end{array} \right) }_{\mathrm{TILT}} \underbrace{ \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{array} \right) }_{\mathrm{ROLL}} \underbrace{ \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & k & 0 \\ 0 & 0 & k \end{array} \right) }_{\mathrm{ZOOM}} \left( \begin{array}{c} R \\ u \\ v \end{array} \right) \end{align}

　上記の変換式により、ディスプレイ上の座標、すなわち接平面上の座標$(u, v)$から3次元空間上の座標 $(x', y', z')$が算出されます。次に球面スクリーン上の対応する座標$(x'', y'', z'')$を計算します。 点 $(x', y', z')$と原点$O$を結んだ直線と球面との交点が求める点$(x'', y'', z'')$となるので、 以下の式で座標を計算できます。

\[ x'' = \frac{Rx'}{\sqrt{x'^2 + y'^2 + z'^2}} \hspace{20pt} y'' = \frac{Ry'}{\sqrt{x'^2 + y'^2 + z'^2}} \hspace{20pt} z'' = \frac{Rz'}{\sqrt{x'^2 + y'^2 + z'^2}} \]

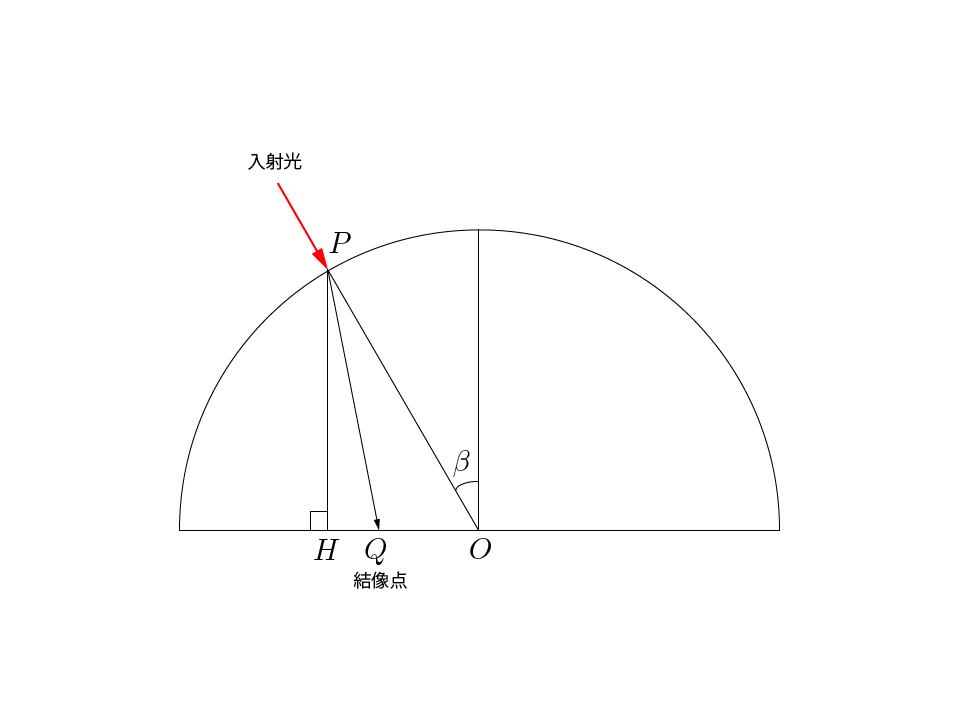
　最後にCCDやCMOSの撮像素子上の座標$(x, y)$を求めるわけですが、レンズごとに像高特性というものが あり、像高特性によって算出方法が変わります。像高特性とは、撮像素子上にできる円画像の中心から入射光 の結像点までの距離と入射光の球面スクリーン上の交点から撮像素子への垂線の足までの距離との比です。

　入射光の撮像素子上での結像点を点$Q$とし、入射光と球面スクリーン上の交点$P$から撮像素子への垂線の足を$H$とすると、入射角$\beta$における像高特性$h_{\beta}$は以下の式で表されます。 \[ h_{\beta} = \frac{\overline{OQ}}{\overline{OH}} \] 　球面スクリーン上の座標$(x'', y'', z'')$と像高特性$h_{\beta}$を使うと、撮像素子上の結像点 の座標$(x, y)$は以下の式で求めることができます。 \[ x = x''h_{\beta} \hspace{20pt} y = y''h_{\beta} \] 　像高特性$h_{\beta}$は入射角$\beta$の関数で、どのような関数であるかはレンズの射影方式によって 異なります。入射角$\beta$は以下の式で求めることができます。 \[ \beta = \arccos \left(\frac{z''}{R} \right) = \arccos \left(\frac{z'}{\sqrt{x'^2 + y'^2 + z'^2}} \right) \]

ここで、$\arccos$は$\cos$の逆関数です。

　ここでは、魚眼レンズの射影方式についてご説明します。魚眼レンズの射影方式はいろいろありますが、 代表的な下記の3つについて説明します。

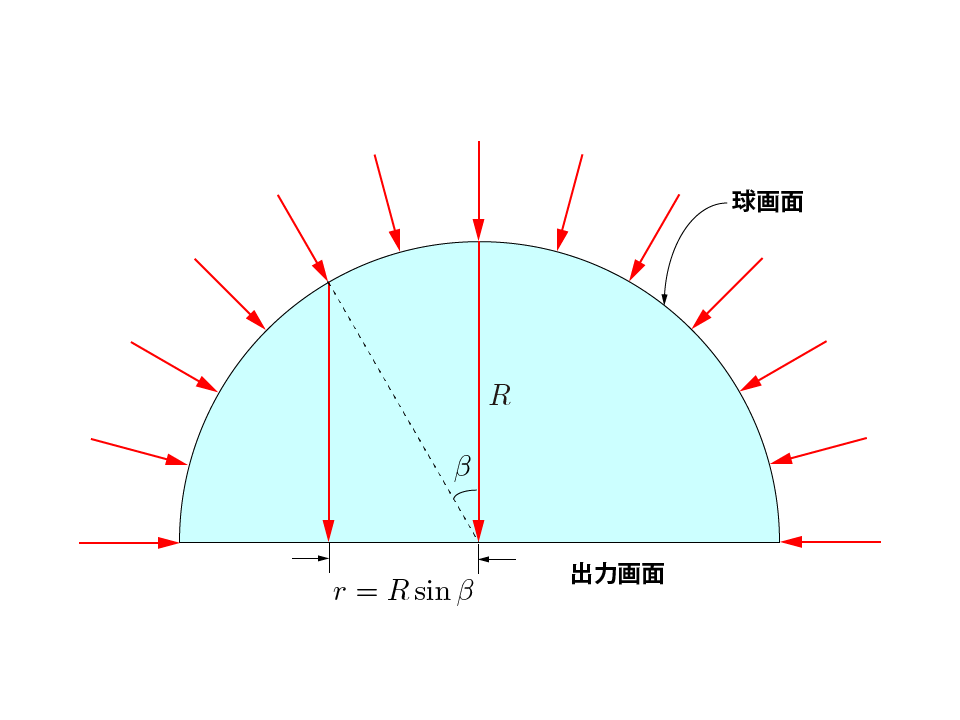
　正射影は、レンズの中心に向かって入射する光線をレンズ内で光軸に平行になるように屈折させる 射影方式です。光軸に対して角度$\beta$で入射した光線はレンズの中心から$R \sin \beta$の地点に 射影されます。正射影による円画像は、球面スクリーンに映し出された画像を真上から見たものと同じ 画像になります。

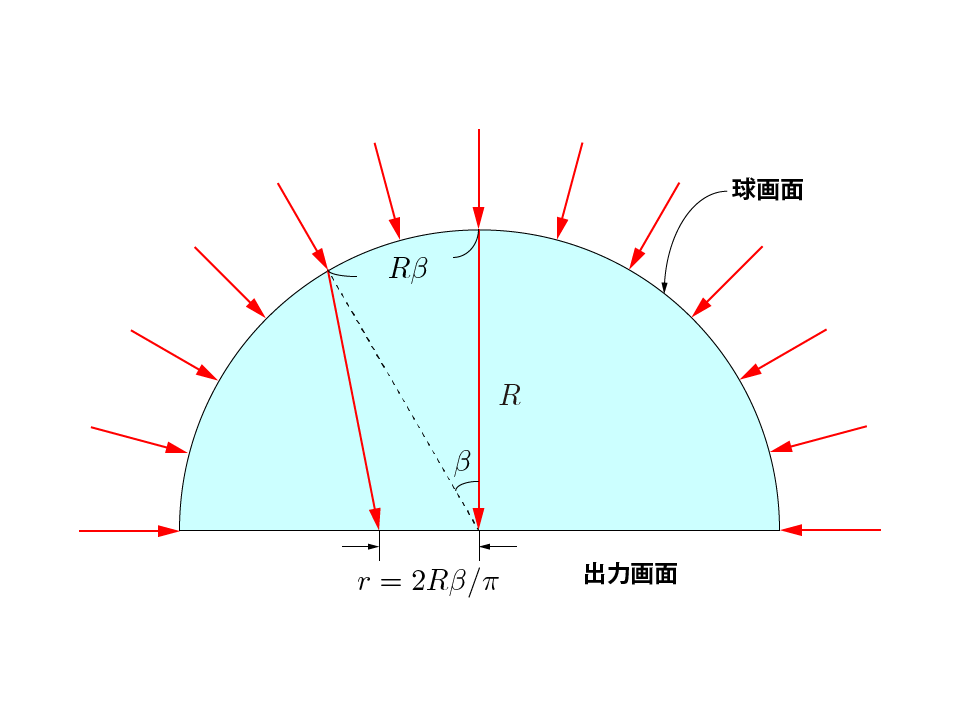
　等距離射影は、レンズへの入射角と、撮像素子上での円画像の中心から像までの距離が比例関係に ある射影方式です。したがって、レンズに対して等間隔の角度で入射した光は、出力画面上でも等間隔に 射影されます。角度$\beta$で入射した光の中心から結像地点までの距離を$r$とすると、$\beta = \pi / 2$ のとき、$r = R$であるので、次のような関係式が成り立ちます。

\[ \beta : r = \pi / 2 : R \]

したがって、角度$\beta$で入射した光は、円の中心から$2R \beta / \pi$の地点に結像します。

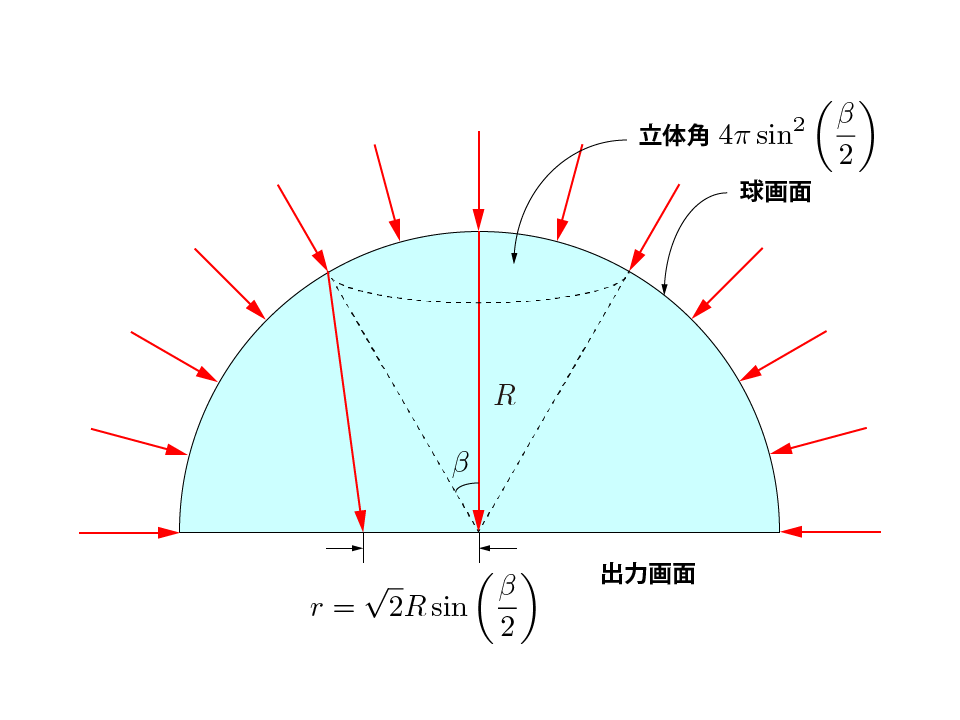
　等立体角射影は等距離射影と出力される画像がよく似ています。等立体角射影とは、光軸に対して角度 $\beta$で入射する光線全体が作る直円錐の球画面から切り取る面積と、出力画面上で射影点全体が作る円の 面積が比例関係にある射影方式です。

　入射角$\beta$の光線全体が球画面から切り取る面積は、

\begin{align} \int^{\beta}_{0} 2 \pi R^2 \sin \varphi \ d \varphi &= 2 \pi R^2 (1 - \cos \beta) \\ &= 4 \pi R^2 \sin^2 \frac{\beta}{2} \end{align}

となります。射影された円の半径を$r$とすると、円の面積は$\pi r^2$です。$\beta = \pi / 2$ のとき半球面が切り取られるので、面積は$2 \pi R^2$となります。したがって、以下のような比例関係が 成り立ちます。

\begin{align} \pi r^2 : 4 \pi R^2 \sin^2 \frac{\beta}{2} &= \pi R^2 : 2 \pi R^2 \\ \end{align}

したがって、角度$\beta$で入射した光線は中心から$r = \sqrt{2} R \sin \frac{\beta}{2}$の 地点に射影されます。